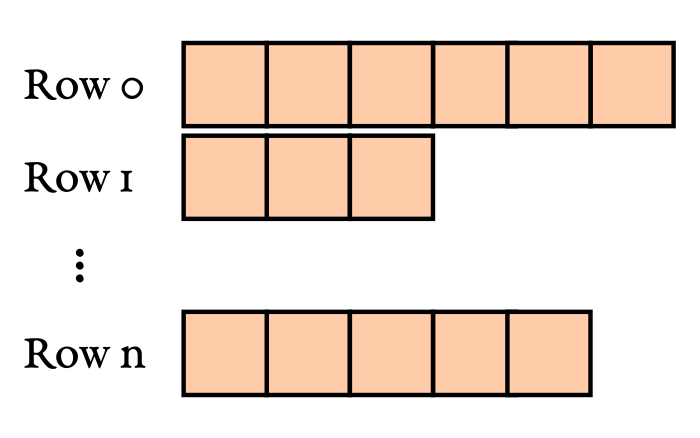
In high energy physics, a lot of data is presented in the form of ragged or
jagged arrays. Often each row represents an event produced by the collision of
highly energetic particles at a particle accelerator. The number of items per row
depends on the event itself. For example, this could depend on the number of
jets produced in a proton-proton interaction at the LHC. Awkward array’s
JaggedArray makes working with these data structures easy and performant in
Python.
A lot of tasks can be easily implemented in a vector-like fashion, such that high-level operations are executed on many/all elements at once as it is the case for numpy arrays. For some tasks, such an implementation is very difficult. In such cases, one resorts back to looping over every row and every item. Could this be speed-up by using numba? Well, good question.
Let’s assume we have a JaggedArray and we want to compute a single quantity
for each row. For the sake of this article, let’s assume we want to compute the
signum of the
permutation which sorts each row. This means we want to compute
-1if we need an odd number of swaps in order to sort the row,+1if we need an even number of swaps in order to sort a row, and0if the input array contains duplicates orNaNs.
The Task
import math
import numpy as np
def signum(array):
"""
Returns the signum of the permutation required to sort the array, i.e. it
returns
* -1 if an odd number of swaps is required to sort the array,
* +1 if an even number of swaps is required to sort the array, and
* 0 if the input array contains duplicates or NaNs.
"""
array = list(array) # Copy array
i = 0
swaps = 0
while True:
if i + 1 >= len(array):
# Exit condition, stop if reached last item
break
# Check for NaN, ordering is not well defined with NaNs
if math.isnan(array[i]):
return 0
if math.isnan(array[i + 1]):
return 0
if array[i] == array[i + 1]:
# Duplicated entry
return 0
if array[i] > array[i + 1]:
# Require swap, move index back by one place
array[i], array[i + 1] = array[i + 1], array[i]
swaps += 1
i -= 1
else:
# Everything is in order, move to next item
i += 1
if i < 0 :
# Make sure we don't go before first item
i = 0
if swaps % 2 == 0:
# Even permutation required to sort list
return +1
# Odd perumutation required to sort list
return -1
The implementation might look long and complicated the but logic behind it is rather simple. Let’s look at some examples.
The list [1, 2, 3, 4] is already sorted, so we don’t need any swaps. Since
zero is an even number, the method returns 1.
>>> signum([1, 2, 3, 4])
1
For the list [1, 3, 2, 4] we need to swap 3 and 2 in order to arrive at an
ordered list. So, there is an odd number of swaps, thus the method returns -1.
>>> signum([1, 3, 2, 4])
-1
This method might be very useful for real-life applications, but it nicely illustrates computational tasks that are not easily implemented in a vector-like fashion.
Loop approach
How should we loop over the jagged array? The simplest solution is by using a good, old loop in Python.
jagged_array = get_jagged_array() # 20_000 rows, 0-100 items per row
def get_signs_loop(jagged_array):
signs = np.empty(len(jagged_array))
for i, row in enumerate(jagged_array):
signs[i] = signum(row)
return signs
On my machine, this takes around 25s. So it seems like there is plenty of room for improvements.
Naive numba approach
One instinct might be to wrap everything by a numba just-in-time compilation.
import numba
jagged_array = get_jagged_array() # 20_000 rows, 0-100 items per row
@numba.njit
def get_signs_loop(jagged_array):
signs = np.empty(len(jagged_array))
for i, row in enumerate(jagged_array):
signs[i] = signum(row)
return signs
This, however, will not work. The reason is that numba doesn’t know (yet) how to
work with JaggedArrays.
“Jagged loop” approach
There is an alternative approach that will make sure that numba can work on
plain numpy arrays. Jagged arrays give access to all its content via the
content property. The lengths of the rows are stored in the counts property.
Both are numpy arrays. We can construct a JITed wrapper taking these arrays as
input, which then slices the content array and passes the slices to the signum
defined above.
We can even go one step further and package all of this in a decorator.
from functools import wraps
import numba
import numpy as np
def jagged_loop(func):
"""
Function decorator. Returns a function which accepts a JaggedArray. The
function loops over the array and passes each row to the decorated
function.
"""
func = numba.njit(func)
@numba.njit
def main_loop(content, counts):
cum_counts = counts.cumsum()
length = len(counts)
result = np.empty(length, dtype=content.dtype)
for i in range(length):
start = cum_counts[i] - counts[i]
end = cum_counts[i]
result[i] = func(content[start:end])
return result
@wraps(func)
def wrapper(array):
return main_loop(array.content, array.counts)
return wrapper
The final main then looks as follows.
@jagged_loop
def signum(array):
"""
Returns the signum of the permutation required to sort the array, i.e. it
returns
* -1 if an odd number of swaps is required to sort the array,
* +1 if an even number of swaps is required to sort the array, and
* 0 if the input array contains duplicates or NaNs.
"""
... see code from above ...
jagged_array = get_jagged_array() # 20_000 rows, 0-100 items per row
def get_signs_jloop(jagged_array)
return signum(jagged_array) # Will loop over rows!
The runtime of get_signs_jloop() is a whopping 70ms. This means we were
able to speed up the signum
computation of a jagged array by a factor of more than 350 compared to plain python
loops.
This might also interest you
